« Back to tutorial listing

— A simple turn-based strategy game —
Part 15: Map generation

Note: this tutorial assumes knowledge of C, as well as prior tutorials.

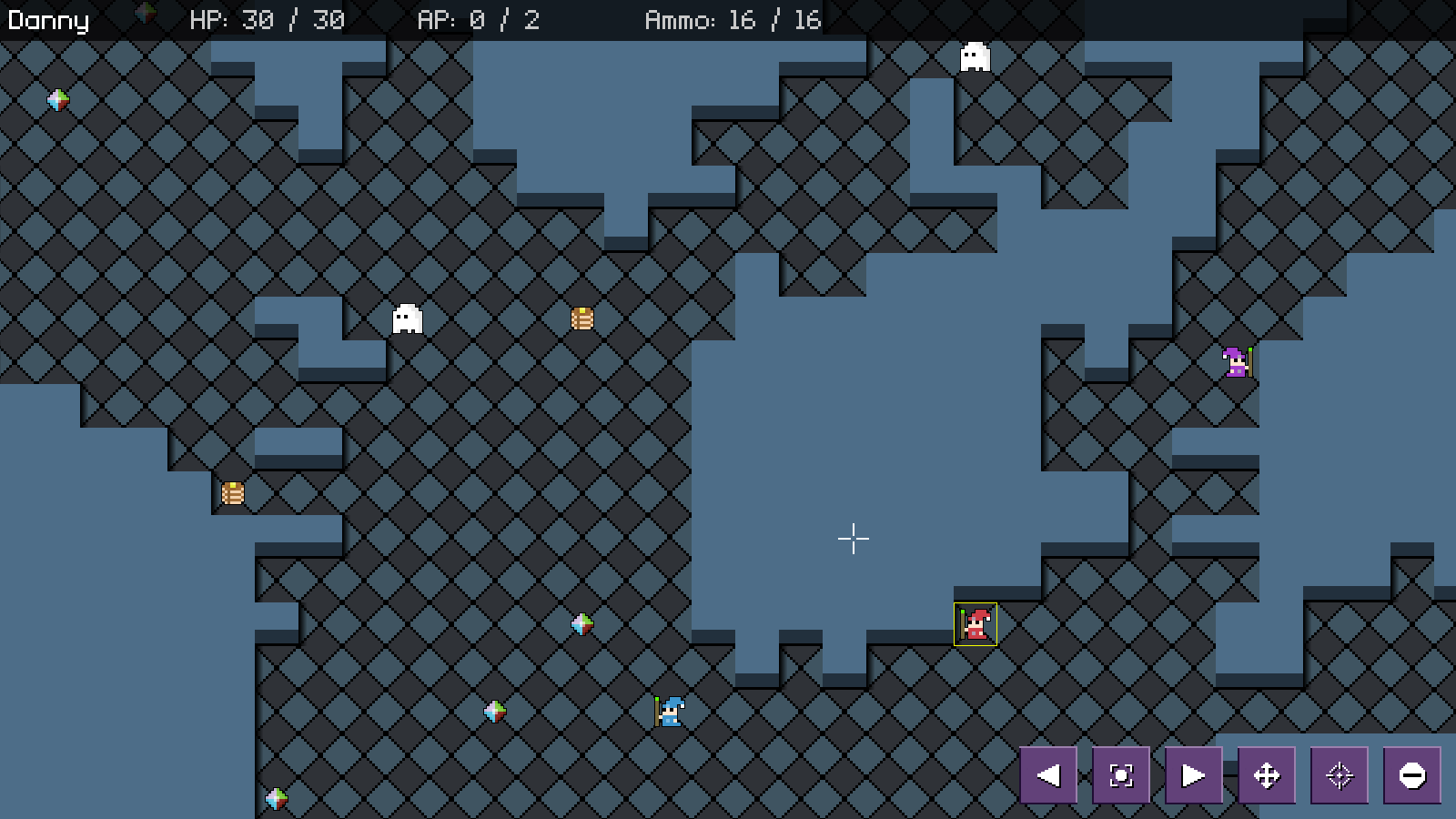
Introduction

Up until now, we've been playing the game on a small, rather badly laid out map. In this part, we're going to generate one that is a bit more pleasing to explore.

Extract the archive, run cmake CMakeLists.txt, followed by make, and then use ./sdl2TBS15 to run the code. You will see a window open like the one above, showing three wizards in a maze-like map, as well as a number of ghosts. Play the game as normal. Notice how the layout of the map changes each time, but always has a vast area in which the player can explore. Once you're finished, close the window to exit.

Inspecting the code

Our map is going to be generated using a technique known as cellular automata. This is a popular method of map generation, that typically results in a cave-like output. This is different to the drunk-walk technique that we used in SDL2 Rogue. Due to the nature of the generation approach, not all of the map will be accessible. Therefore, we'll be employing several additional steps, to ensure that the player isn't boxed away from the main map.

Starting with defs.h:

#define MAP_WIDTH                 80
#define MAP_HEIGHT                40

We've just increased the size of the map. We could make this even larger if we desired, but keep in mind that it would lead to repetiton quite quickly.

Now, moving over to mapGen.c. This is where the main focus on this part will be. Let's start with generateMap:

void generateMap(void)
{
	do
	{
		doCellularAutomata();
	} while (!verifyCapacity());

	decorate();
}

This function is called my initStage and is responsible for our map generation. We're calling doCellularAutomata in a while-loop, that depends on the outcome of verifyCapacity in order to exit. The reason for this is because the map generated by doCellularAutomata might not meet our criteria; verifyCapacity will test to see if the map allows for a certain level of exploration, based on a start point, and if not it will reject the map. Finally, `decorate` will be called to update the walls, to make them appear a little less flat.

Coming first to doCellularAutomata:

static void doCellularAutomata(void)
{
	int i, x, y, n;
	MapTile **tmp;

	tmp = malloc(sizeof(MapTile*) * MAP_WIDTH);

	// randomize
	for (x = 0 ; x < MAP_WIDTH ; x++)
	{
		tmp[x] = malloc(sizeof(MapTile) * MAP_HEIGHT);

		memset(tmp[x], 0, sizeof(MapTile) * MAP_HEIGHT);

		for (y = 0 ; y < MAP_HEIGHT ; y++)
		{
			if (rand() % 100 < 40)
			{
				tmp[x][y].tile = 1;
			}
		}
	}

	// smooth
	for (i = 0 ; i < 3 ; i++)
	{
		for (x = 0 ; x < MAP_WIDTH ; x++)
		{
			for (y = 0 ; y < MAP_HEIGHT ; y++)
			{
				stage.map[x][y].tile = 0;

				n = countNeighbours(tmp, x, y);

				if (n > 3)
				{
					stage.map[x][y].tile = 1;
				}
			}
		}

		for (x = 0 ; x < MAP_WIDTH ; x++)
		{
			for (y = 0 ; y < MAP_HEIGHT ; y++)
			{
				tmp[x][y] = stage.map[x][y];
			}
		}
	}

	for (x = 0 ; x < MAP_WIDTH ; x++)
	{
		free(tmp[x]);
	}

	free(tmp);
}

This function is our main cellular automata step. It can be considered to be split into three sections. We'll go through these one at a time.

First, we're mallocing an array of MapTiles of MAP_WIDTH length (as `tmp`). We're then entering into a for-loop, and, for each row, allocating an array of MapTiles of length MAP_HEIGHT to each row index. In short, we're creating another set of map data, as temporary storage. With that done, there's a 40% chance that we're going to set the value of the MapTile at the current x/y index to 1. So, 40% of our map will have a tile value of 1, the rest 0.

The next step is the smooth step. Right now, our map is a random scattering of 0s and 1s. We want to erode and replace some of these values, keeping only those who meet certain criteria. Basically, we're going to loop through each value in our temporary map and count the number of surrounding tiles with a value of 1 (via countNeighbours). The result is assigned to a variable called `n`. If the value of `n` is greater than 3, we're going to set the value of Stage's map as the same index as `tmp` to 1. By default, the value is 0.

Something important now - we're evaluating the temporary map and updating Stage's map! It's important not to update the map we're testing as we go along, as this will lead to unexpected results. In short, the data we're testing would be changing under our feet, and we need it to be atomic, hence the reason we're working on a copy.

Once we've been through `tmp`'s values and updated Stage's map's value, we then setup another couple of for-loops to copy Stage's map data into `tmp`'s map data. The reason for this is because we're going to be performing this smoothing step 3 times, and so we need to copy all the changes from Stage's map back into `tmp`, so at the commencement of the next loop we're working with up-to-date data.

With that done, we're freeing all of `tmp`'s data, to ensure we don't leak memory. At the end of this function, Stage's map will contain a map with a cave-like appearance. However, there is a problem - part of the map will be alcoves that will be cut off from the main body. We don't want this, as it means that game elements could be randomly inserted there and be inaccessible. Bad if it's a ghost, even worse if it's where the player's party starts. We'll see how we overcome this in a moment.

First, let's look at countNeighbours:

static int countNeighbours(MapTile **data, int mx, int my)
{
	int x, y, tx, ty, n;

	n = 0;

	for (x = -1 ; x <= 1 ; x++)
	{
		for (y = -1 ; y <= 1 ; y++)
		{
			if (x != 0 || y != 0)
			{
				tx = mx + x;
				ty = my + y;

				if (isInsideMap(tx, ty) && data[tx][ty].tile == 1)
				{
					n++;
				}
			}
		}
	}

	return n;
}

Quite straightforward. We're passing over the temporary map data (`data`), and the location of the map that we want to count the surrounding tiles from (`mx` and `my`). We do so by setting a variable called `n` to 0. This will represent the number of neighbours. We then use two for-loops on the `x` and `y` (-1 to 1, inclusive), to check the surrounding tiles. We ignore the centre tile (the one we're counting the neighbours for). We check the value of the surrounding tile, and if it's 1, we'll increment the value of `n`. Finally, we'll return `n`, which will be the count of the number of surrounding tiles with a value of 1.

So, if a tile has 4 or more neighbours with a value of 1, it will become or remain a 1 in our Stage's map data. Otherwise, it will become a 0. So, map tiles not connected to many others will be destroyed, and holes will be plugged. This is somewhat like Conway's Game of Life.

Now, let's turn to verifyCapacity:

static int verifyCapacity(void)
{
	int x, y, fillCount, attempts;
	double fillPercent;

	attempts = 0;

	do
	{
		x = rand() % MAP_WIDTH;
		y = rand() % MAP_HEIGHT;

		if (stage.map[x][y].tile == 1)
		{
			fillCount = floodFill(x, y, 1, 2);

			fillPercent = (1.0 * fillCount) / (MAP_WIDTH * MAP_HEIGHT);

			if (fillPercent < REQUIRED_FLOOD_FILL_PERCENT)
			{
				if (++attempts >= 25)
				{
					return 0;
				}

				floodFill(x, y, 2, 1);
			}
		}
	}
	while (fillPercent < REQUIRED_FLOOD_FILL_PERCENT);

	for (x = 0 ; x < MAP_WIDTH ; x++)
	{
		for (y = 0 ; y < MAP_HEIGHT ; y++)
		{
			if (stage.map[x][y].tile == 2)
			{
				stage.map[x][y].tile = TILE_GROUND;
			}
			else
			{
				stage.map[x][y].tile = TILE_WALL;
			}
		}
	}

	return 1;
}

The idea behind this function is to ensure that we have enough connected ground tiles (seen as 1s in the map data), to provide a map that can be navigated. Inaccessible areas will be sealed off. This is achieved by flood filling random areas of the map, and counting how many tiles were affected.

We start by setting a variable called `attempts` to 0. This will control the number of attempts we've made to fill a suitably sized location of the map, at random. Next, we enter into a while-loop, where we randomly select an array of the map (`x` and `y`), checking that it's a MapTile with value 1, and then call a function named floodFill. We'll see more on this in a bit, but basically it attempts to convert tiles of value 1 to value 2. The function returns the number of tiles that it filled. With this, we work out the percentage cover of the map (as a value between 0 and 1) and test whether it met the percentage we need to consider the map usable (REQUIRED_FLOOD_FILL_PERCENT). If not, we'll test to see if we've exceeded our number of fill attempts, and exit the function by returning 0. Otherwise, we'll call floodFill again, to flip our 2s back to 1s.

If our flood fill criteria is met, we'll loop through our map data and convert all the map tile with a value of 2 into TILE_GROUND. Everything else will have a value of TILE_WALL.

So, in summary - we're randomly picking a spot on the map, flood filling it to see how much of it is connected to the rest of the map, and converting the tiles to floors and walls, to turn it into a proper map.

Now let's look at floodFill:

static int floodFill(int x, int y, int from, int to)
{
	int fillCount;
	Node *n;

	memset(&fillHead, 0, sizeof(Node));

	fillTail = &fillHead;

	addFillNode(x, y, from);

	fillCount = 0;

	while (fillHead.next != NULL)
	{
		n = fillHead.next;

		stage.map[n->x][n->y].tile = to;

		fillCount++;

		addFillNode(n->x + 1, n->y, from);
		addFillNode(n->x - 1, n->y, from);
		addFillNode(n->x, n->y + 1, from);
		addFillNode(n->x, n->y - 1, from);

		fillHead.next = n->next;

		free(n);
	}

	return fillCount;
}

We'll not linger on this, as it's basically just an implementation of a flood fill, using a queue. The function takes four parameters: `x` and `y`, the starting location on Stage's map data; and `from` and `to`, the tile value we want to convert from and to (example, 1 and 2). Our flood fill is achieved by using a queue (fillTail and fillHead), in a similar fashion to evaluating our units' move range.

The queue is appended to using a function named addFillNode:

static void addFillNode(int x, int y, int from)
{
	Node *n;

	if (isInsideMap(x, y) && stage.map[x][y].tile == from)
	{
		for (n = fillHead.next ; n != NULL ; n = n->next)
		{
			if (n->x == x && n->y == y)
			{
				return;
			}
		}

		n = malloc(sizeof(Node));
		memset(n, 0, sizeof(Node));
		fillTail->next = n;
		fillTail = n;

		n->x = x;
		n->y = y;
	}
}

Again, this function is quite similar to the one we use in units.c. Basically, we're testing that the map location we wish to add to our queue (`x` and `y`) lies within the map and is of the tile type we want to convert (`from`). We next test that the node doesn't already exist in our queue, and add it as needed.

The last function is `decorate`:

static void decorate(void)
{
	int x, y;

	for (x = 0 ; x < MAP_WIDTH ; x++)
	{
		for (y = 0 ; y < MAP_HEIGHT ; y++)
		{
			// lower wall portion
			if (stage.map[x][y].tile == 0 && y < (MAP_HEIGHT - 1) && stage.map[x][y + 1].tile != 0)
			{
				stage.map[x][y].tile = 1;
			}

			// right-hand wall shadow
			if (stage.map[x][y].tile == 5 && x > 0 && stage.map[x - 1][y].tile < 5)
			{
				stage.map[x][y].tile = 6;
			}
		}
	}
}

This function is merely responsible for updating some of the wall and ground tiles to use different images, depending on what they are close to. We loop through all whole map, searching for tiles and their neighbours that fit the if-statements, and update the tile value accordingly. For example, we're changing a ground tile that neighbours a wall to use the image that has a shadow, to give some depth. Not a lot more to say here, as decorating the map is mainly about styling.

That's our map generation done! As you can see, we're simply implementing a cellular automata function, and then cleaning things up, to make it usable. With that done, there are a couple of other things we need to address.

Heading over to player.c, we've updated addPlayerUnits:

static void addPlayerUnits(void)
{
	Entity *e;
	int i, mx, my, x, y, ok;
	char *names[] = {"Andy", "Danny", "Izzy"};

	do
	{
		mx = rand() % MAP_WIDTH;
		my = rand() % MAP_HEIGHT;
	}
	while (!isGround(mx, my));

	for (i = 0 ; i < NUM_PLAYER_UNITS ; i++)
	{
		e = initEntity(names[i]);

		e->side = SIDE_PLAYER;

		do
		{
			x = mx + rand() % 3 - rand() % 3;
			y = my + rand() % 3 - rand() % 3;

			ok = isGround(x, y) && getEntityAt(x, y) == NULL;
		}
		while (!ok);

		e->x = x;
		e->y = y;

		units[i] = e;
	}

	stage.currentEntity = units[0];

	updateUnitRanges();

	ensureOnScreen(stage.currentEntity);
}

Since our map now contains many more walls, we need to ensure that our starting location lies within an open area. We do this by first setting up a while-loop to look for a starting location on the map (as `mx` and `my`) that that the mages can stand on (isGround). We keep updating `mx` and `my`, and testing the location until we find a valid point. `mx` and `my` will be the point around which we'll add our units. Now, when setting the player unit's `x` and `y`, we'll take `mx` and `my`, and randomly add a value between -3 and +3. This basically gives us a radius to work with.

Finally we've updated ghosts.c:

void initWhiteGhost(Entity *e)
{
	Unit *u;

	STRCPY(e->name, "White Ghost");

	u = initGhost(e, "gfx/units/whiteGhost.png");
	u->hp = u->maxHP = 10;
	u->ap = u->maxAP = 2;
	u->moveRange = 12;

	u->ai.type = AI_PASSIVE;
}

We've updated the unit's ai type to AI_PASSIVE, so our white ghosts are once again passive spirits, who will wander the map and not react to the mages, at all.

That's our map generation done! We've now got something more interesting to work with. Of course, there is plenty more that could be done with our map generation to make things even better, but what we have here is enough for now and a great starting point.

Speaking of interesting things, how about we add in MapTiles that the ghosts can move across, but the player cannot? A hazard, if you will. In the next part, we're going to look at adding in slime tiles. These tiles will block the mage's movement, but allow the ghosts free passage (as they can just float over the top). However, the mages won't be at a complete loss, as they will be able to target the slime tiles and destroy them!

Purchase

The source code for all parts of this tutorial (including assets) is available for purchase:

From itch.io

It is also available as part of the SDL2 tutorial bundle: